[ad_1]
Você sabia que os objetos ao seu redor, como armários, escrivaninhas, livros e assim por diante, são espaços de construção? É chamado de formato de espaço porque esses objetos têm comprimento, largura e altura, de modo que podem determinar o volume e a área da superfície do objeto. Em matemática, uma das formas dos espaços é um prisma. Nesta discussão, tentaremos entender como determinar o volume de um prisma. Vamos, ouça!
Uma forma tem volume, que é a quantidade de substância ou objeto que pode preencher a forma. Quanto maior o tamanho de um edifício, maior seu volume. O prisma em si pode ser interpretado como um espaço limitado por duas formas planas congruentes e paralelas conectadas por nervuras verticais.
Como você sabe, a nomenclatura do prisma seguirá o formato da base. Se a base do prisma for retangular, o prisma tem um nome especial, que é feixe. Enquanto isso, um prisma com um lado quadrado é conhecido como cubo.
(Leia também: Fórmulas de volume de cubo e exercícios de exemplo)
Na fórmula do volume de um bloco, a base do bloco é um retângulo, que tem a fórmula comprimento da área vezes largura. Já na fórmula do volume para um cubo, a base do cubo é um quadrado que tem a fórmula para a área dos lados vezes os lados. Com base nessas duas fórmulas, pode-se concluir que a fórmula para determinar o volume de um prisma é Área da Base x Altura do Prisma
Exemplo de problemas:
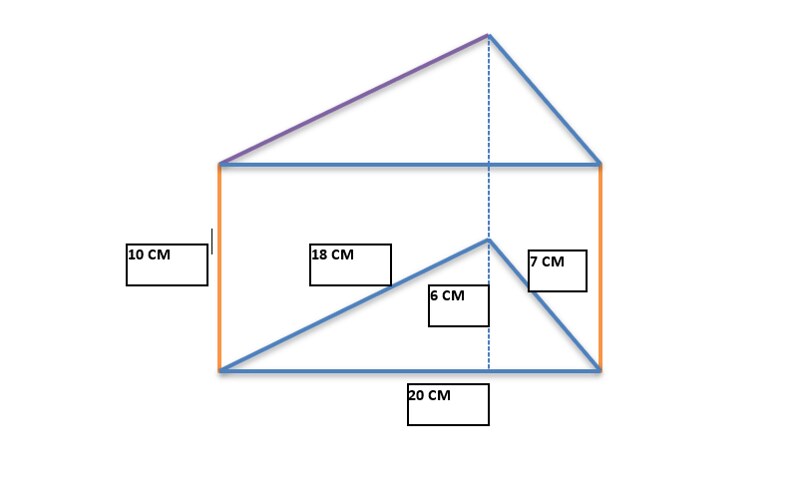
- Calcule o volume do seguinte prisma triangular!
Solução:
Dado que a base do prisma é essa quantidade, o volume do prisma é:
Área da base = Área do triângulo
= 1/2 x a x t
= 1/2 x 20 x 6
= 60 cm2
Então, o volume do prisma = Luma x tprisma
= 60 x 10
= 600 cm3
- Dado que o volume do prisma seguinte é 4500 m3, determine a altura do prisma!
Solução:
Dado que a base do prisma é um triângulo,
Área da base = Área do triângulo
= 1/2 x a x t
= 1/2 x 25 x 12
= 150 cm2
Assim, o volume do prisma = Luma x tprisma
4500 = 150 x tprisma tprisma
= 4500: 150 = 30 m
Portanto, a altura do prisma é de 30 metros
Siga-nos e curta-nos:
[ad_2]
Source link
