Arquimedes – Enciclopédia do Novo Mundo

Arquimedes (Grego: Ἀρχιμήδης) (cerca de 287 A.E.C. -212 A.E.C.) foi um matemático, físico, engenheiro, astrônomo e filósofo da Grécia Antiga, considerado um dos maiores matemáticos da antiguidade. Arquimedes aparentemente estudou matemática em Alexandria, mas viveu a maior parte de sua vida em Siracusa. Ele descobriu como encontrar o volume de uma esfera e determinou o valor de Pi; desenvolveu uma maneira de contar usando zeros para representar potências de dez; descobriu uma fórmula para encontrar a área sob uma curva e a quantidade de espaço delimitado por uma curva; e ele pode ter sido o primeiro a usar o cálculo integral. Arquimedes também inventou o campo da estática, enunciou a lei da alavanca, a lei do equilíbrio dos fluidos e a lei da flutuabilidade. Ele foi o primeiro a identificar o conceito de centro de gravidade e encontrou os centros de gravidade de várias figuras geométricas, incluindo triângulos, parabolóides e hemisférios, assumindo a densidade uniforme de seus interiores. Usando apenas a geometria grega antiga, ele também deu as posições de equilíbrio das seções flutuantes dos parabolóides com base em sua altura, um feito que seria desafiador para um físico moderno que usa cálculo.

Arquimedes só se tornou amplamente conhecido como matemático depois que Eutocius publicou edições de algumas de suas obras, com comentários, no século VI. CE. Os escritores antigos estavam mais interessados ​​em suas invenções e nas engenhosas máquinas de guerra que ele desenvolveu do que em suas realizações em matemática. Plutarco relata como as máquinas de guerra de Arquimedes defenderam Siracusa contra os atacantes romanos durante a Segunda Guerra Púnica. Muitas das obras de Arquimedes foram perdidas quando a Biblioteca de Alexandria queimou (duas vezes) e sobreviveu apenas em traduções latinas ou árabes.

Tempo de vida

Arquimedes nasceu na colônia portuária de Siracusa, Magna Graecia (atual Sicília), por volta de 287 A.E.C. Ele estudou em Alexandria e depois voltou para Siracusa, onde passou o resto de sua vida. Muito do que se sabe sobre Arquimedes vem dos prefácios de suas obras e das histórias relatadas por Plutarco, Tito Lívio e outros historiadores antigos. O prefácio de O contador de areia diz-nos que o pai de Arquimedes, Fídias, era astrônomo. No prefácio de Em espirais, Arquimedes relata que costumava enviar declarações de seus últimos teoremas aos amigos em Alexandria, mas sem apresentar provas. Alguns dos matemáticos reivindicaram seus resultados como seus próprios, então Arquimedes diz que a última vez que ele enviou teoremas ele incluiu dois que eram falsos, “… de modo que quem afirma ter descoberto tudo, mas não apresenta prova do mesmo, pode ser refutado como se pretendesse descobrir o impossível.Ele considerava Conon de Samos, um dos matemáticos alexandrinos, um amigo próximo e o admirava por suas habilidades como matemático.

A dedicação de O contador de areia para Gelon, filho do Rei Hiero, é uma evidência que Arquimedes era próximo à família do Rei Hiero II. A biografia de Plutarco de um soldado romano, Marcelo, que capturou Siracusa em 212 A.E.C., também nos diz que Arquimedes era parente do rei Hiero II de Siracusa. A mesma biografia afirma que Arquimedes, que possuía um espírito elevado e uma alma profunda, recusou-se a escrever qualquer tratado de engenharia ou mecânica, mas preferiu dedicar-se ao estudo da geometria pura e seguiu-o sem se importar com a alimentação ou higiene pessoal. .

E, no entanto, Arquimedes possuía um espírito tão elevado, uma alma tão profunda e uma teoria científica tão rica que, embora suas invenções lhe tivessem ganho um nome e fama por sua sagacidade sobre-humana, 4 ele não consentiria em deixar qualquer tratado sobre Este assunto, mas considerando o trabalho de um engenheiro e toda a arte que atende às necessidades da vida como ignóbil e vulgar, ele dedicou seus esforços sérios apenas aos estudos cuja sutileza e encanto não são afetados pelas demandas da necessidade. Esses estudos, ele pensou, não deveriam ser comparados com outros; nelas o tema concorre com a demonstração, a primeira proporcionando grandeza e beleza, a segunda precisão e potência superior. 5 Porque não é possível encontrar questões mais profundas e difíceis em geometria tratadas em termos mais simples e puros. Alguns atribuem esse sucesso aos seus dons naturais; outros pensam que, por causa do trabalho excessivo, tudo o que ele fazia parecia ter sido feito sem trabalho e com facilidade. Pois ninguém poderia por seus próprios esforços descobrir a prova e, no entanto, assim que a aprende com ele, pensa que poderia tê-la descoberto sozinho; tão suave e rápido é o caminho que leva à conclusão desejada. 6 E, portanto, não podemos deixar de acreditar nas histórias que são contadas sobre ele, como, sob o encanto duradouro de alguma sereia familiar e doméstica, ele esqueceu até mesmo sua comida e negligenciou o cuidado de sua pessoa; e como, quando foi atraído pela força principal, como costumava fazer, para o lugar para se banhar e ungir seu corpo, ele traçou figuras geométricas nas cinzas e traçou linhas com o dedo no óleo com o qual o corpo foi ungido. , possuído por grande deleite, e de fato um cativo das Musas. 7 E embora ele tenha feito muitas descobertas excelentes, diz-se que pediu a seus parentes e amigos que colocassem um cilindro envolvendo uma esfera na sepultura onde deveria ser enterrada, com uma inscrição indicando a proporção em que o conteúdo sólido excede o conteúdo. (Plutarco, Marcelo, 17: 3-7 traduzido por John Dryden)

Plutarco também dá três relatos da morte de Arquimedes nas mãos de soldados romanos. Embora Marcelo tenha ordenado que Arquimedes não fosse ferido, os soldados romanos o encontraram no trabalho e o assassinaram brutalmente. Essas histórias parecem projetadas para contrastar a arrogância dos gregos com a brutalidade insensível e contundente dos soldados romanos.

Mas o que mais afligiu Marcelo foi a morte de Arquimedes. Porque aconteceu que ele estava sozinho, resolvendo algum problema com a ajuda de um diagrama, e tendo fixado seus pensamentos e seus olhos também no assunto de seu estudo, ele não percebeu a incursão dos Romanos ou a tomada do cidade. De repente, um soldado se aproximou dele e ordenou que o acompanhasse até Marcelo. Arquimedes recusou-se a fazer isso até resolver seu problema e estabelecer sua manifestação, 5 após o que o soldado ficou furioso, desembainhou sua espada e o despachou. Outros, porém, dizem que o romano se aproximou dele com a espada desembainhada, ameaçando matá-lo imediatamente, e que Arquimedes, ao vê-lo, implorou fervorosamente que esperasse um pouco, para que não abandonasse o resultado que buscava. incompleto e sem prova; mas o soldado o ignorou e acabou com ele. 6 Há também uma terceira história, que enquanto Arquimedes levava alguns de seus instrumentos matemáticos para Marcelo, como mostradores solares e esferas e quadrantes, por meio dos quais ele tornou a magnitude do sol visível a olho nu, b alguns soldados caíram com ele , e pensando que ele tinha ouro na caixa, ele o matou. No entanto, é geralmente aceito que Marcelo ficou triste até a morte e rejeitou seu assassino como uma pessoa contaminada, e procurou os parentes de Arquimedes e os honrou. (Plutarco, Marcelo, Capítulo 19: 4-6, traduzido por John Dryden)

Pensamento e obras

Arquimedes é considerado pela maioria dos historiadores da matemática um dos maiores matemáticos de todos os tempos. Em criatividade e percepção, Arquimedes superou qualquer outro matemático europeu antes do Renascimento europeu. As obras de Arquimedes não eram geralmente reconhecidas, mesmo na antiguidade clássica, embora as obras individuais fossem frequentemente citadas por três eminentes matemáticos alexandrinos, Heron, Pappus e Theon, e só se tornaram amplamente conhecidas depois que Eutius publicou edições de alguns deles, com comentários, no século VI CE. Muitas das obras de Arquimedes foram perdidas quando a biblioteca de Alexandria queimou (duas vezes) e sobreviveu apenas em traduções latinas ou árabes. Os trabalhos sobreviventes incluem Em balanças planas (Dois livros), Quadratura da parábola, na esfera e no cilindro (Dois livros), Em espirais, Em conóides e esferóides, em corpos flutuantes (Dois livros), Medida de um círculo, Y The Sand Reckoner. No verão de 1906, J. L. Heiberg, professor de filologia clássica na Universidade de Copenhagen, descobriu um manuscrito do século 10 que incluía a obra de Arquimedes. O método, que fornece uma visão notável de como Arquimedes fez muitas de suas descobertas.

Numerosas referências a Arquimedes nas obras de escritores antigos referem-se mais às invenções de Arquimedes, particularmente às máquinas que eram usadas como máquinas de guerra, do que às suas descobertas na matemática.

Invenções

O rei Hiero II, supostamente tio de Arquimedes, o encarregou de projetar e fabricar uma nova classe de navios para sua marinha. Hiero II havia prometido grandes depósitos de grãos aos romanos do norte em troca da paz. Incapaz de entregar a quantia prometida, Hieron II encarregou Arquimedes de desenvolver uma grande e luxuosa barcaça de guerra e suprimentos para sua marinha. O navio, cunhado Saracusia, depois de sua nação, pode ser mítico. Não há registro da arte do casting, nem qualquer outra peça de época que represente sua criação. É apoiado apenas por uma descrição de Platão, que disse que “foi a maior equação já feita”.

Parafuso de arquimedes

O Parafuso de Arquimedes, um dispositivo que puxa água, teria sido desenvolvido como uma ferramenta para remover água de porão de navios. Arquimedes ficou conhecido por sua participação na defesa de Siracusa, na Itália, contra o ataque romano durante a Segunda Guerra Púnica. Em sua biografia de Marcelo, Plutarco descreve como Arquimedes resistiu aos romanos com máquinas de guerra de seu próprio projeto e foi capaz de mover um navio de tamanho real com tripulação e carga com uma polia composta puxando uma única corda.^[1]

7 E, no entanto, até mesmo Arquimedes, que era parente e amigo do rei Hieron, escreveu-lhe que, com qualquer força, era possível mover qualquer peso; e encorajado, como nos é dito, pela força de sua demonstração, ele declarou que se houvesse outro mundo, e ele pudesse ir a ele, ele poderia movê-lo. 8 Hiero ficou pasmo e implorou que colocasse sua proposta em prática e mostrasse um grande peso movido por uma pequena força. Arquimedes, portanto, notou um navio mercante de três mastros da frota real, que havia sido arrastado para terra pelo grande trabalho de muitos homens, e depois de carregar muitos passageiros e a carga usual, sentou-se a alguma distância de ela, e sem grande esforço, mas movendo silenciosamente com a mão um sistema de roldanas compostas, ele a puxou suavemente e uniformemente, como se deslizando na água. 9 Espantado com isso, então, e percebendo o poder de sua arte, o rei persuadiu Arquimedes a preparar para ele máquinas ofensivas e defensivas para serem usadas em todos os tipos de guerra de cerco. Ele mesmo nunca os havia usado, porque passou a maior parte de sua vida livre da guerra e em meio aos festivos ritos de paz; mas hoje seu aparelho serviu aos siracusanos e, com o aparelho, a seu fabricante. Plutarco, Capítulo 14, Marcelo, 7-9

Garra de Arquimedes

Uma de suas invenções usadas para a defesa militar de Siracusa contra os invasores romanos foi a “Garra de Arquimedes”. Arquimedes também é creditado por melhorar a precisão, alcance e potência da catapulta, e a possível invenção do hodômetro durante a Primeira Guerra Púnica.

15 Portanto, quando os romanos os atacaram por terra e mar, os siracusanos ficaram mudos de terror; Eles pensaram que nada poderia resistir a um ataque tão furioso por tais forças. Mas Arquimedes começou a operar seus motores e disparou contra as forças terrestres dos assaltantes todos os tipos de projéteis e imensas massas de pedras, que caíram com incrível ruído e velocidade; nada poderia evitar seu peso, mas eles derrubaram aqueles que estavam em seu caminho e confundiram suas fileiras. 2 Ao mesmo tempo, de repente enormes vigas foram projetadas sobre os navios das paredes, afundando alguns deles com grandes pesos caindo do alto; Outros foram agarrados na proa por garras de ferro ou picos como bicos de guindastes, erguidos no ar e depois afundados pela popa nas profundezas, ou girados e girados por meio de engenharia dentro da cidade, e lançado sobre os penhascos íngremes que se projetavam sob a muralha da cidade, para grande destruição dos guerreiros a bordo, que morreram nos naufrágios. 3 Freqüentemente, também, um navio saía da água no ar, girava de um lado para o outro enquanto estava pendurado ali, uma visão hedionda, até que sua tripulação fosse atirada em todas as direções, quando ficava vazio. nas paredes, ou deslize para longe da embreagem que o segurava. Quanto à locomotiva que Marcelo escalou na ponte dos botes, e que se chamava “sambuca” por alguma semelhança que tinha com o instrumento musical de mesmo nome, 25 4 quando ainda estava a certa distância na abordagem da parede, ele Ele atirou nele uma pedra de dez talentos26, depois uma segunda e uma terceira; Alguns deles, caindo sobre ele com grande estrondo e maremoto, esmagaram os alicerces da locomotiva, destruíram sua estrutura e a arrancaram da plataforma, de modo que Marcelo, perplexo, ordenou que seus navios voltassem o mais rápido que pudessem, e seu terreno forças para se retirar.

5Então, em uma corte marcial, foi decidido passar por baixo das paredes enquanto ainda era noite, se pudessem; porque as cordas que Arquimedes usava nas suas máquinas, dado que davam grande ímpeto ao lançamento dos mísseis, pensavam que os fariam voar por cima das suas cabeças, mas seriam ineficazes à queima-roupa, onde não havia lugar para o lançamento. Arquimedes, no entanto, aparentemente havia se preparado muito antes para tal emergência, motores com um alcance adaptado a qualquer intervalo e mísseis de voo curto, e através de muitas aberturas pequenas e contíguas na parede eles poderiam ser carregados para o motores de curto alcance chamados escorpiões. Apoie-se em objetos próximos sem ser visto pelo inimigo. Quando, portanto, os romanos escalaram por baixo das muralhas, acreditando não serem notados, mais uma vez encontraram uma grande tempestade de mísseis; pedras enormes caíram sobre eles quase perpendicularmente, e a parede atirou flechas neles de todos os pontos; portanto, eles se retiraram. 2 E aqui novamente, quando eles estavam a alguma distância, os projéteis dispararam e caíram sobre eles quando eles se afastaram, e houve uma grande matança entre eles; muitos de seus navios também se chocaram e foram incapazes de retaliar de forma alguma contra seus inimigos. Como Arquimedes havia construído a maioria de suas máquinas perto da parede, e os romanos pareciam estar lutando contra os deuses, agora que incontáveis ​​travessuras foram derramadas sobre eles de uma fonte invisível.

17 No entanto, Marcelo escapou, brincando com seus próprios artesãos e engenheiros: “Vamos parar”, disse ele, “lutando contra esse Briareo geométrico, que usa nossos navios como taças para tirar água do mar, e espancou e expulsou nossos sambuca, e com os muitos mísseis que atira em nós ao mesmo tempo, supera os monstros da mitologia de cem mãos. ” 2 Porque, na realidade, o resto dos Siracusanos não eram nada mais do que um corpo para os projetos de Arquimedes, e sua alma era a única que movia e gerenciava tudo; porque todas as outras armas estavam ociosas, e somente as delas eram usadas pela cidade tanto no ataque quanto na defesa. 3 Por fim, os romanos ficaram com tanto medo que, ao verem um pedaço de corda ou um pedaço de pau que se projetava um pouco da parede, gritaram: “Lá está ele”, “Arquimedes está preparando uma máquina para nós”, deram as costas e fugiram. Vendo isso, Marcelo desistiu de todas as lutas e assaltos, e desde então passou a depender de um longo cerco. (Plutarco, Marcelo, Capítulos 15 – 17

Raio da morte

Um diagrama mostrando como Arquimedes pode ter permitido que os defensores de Siracusa apontassem seus espelhos para os navios que se aproximavam.

Diz-se que Arquimedes evitou um ataque romano a Siracusa usando uma variedade de espelhos (especulados para serem escudos altamente polidos) para refletir a luz solar concentrada sobre os navios atacantes, fazendo com que pegassem fogo. Esta lenda popular, apelidada de “raio da morte de Arquimedes”, foi comprovada muitas vezes desde a Renascença e muitas vezes desacreditada. Parece que os navios deveriam estar praticamente imóveis e muito próximos da costa para pegar fogo, um cenário improvável durante uma batalha. Um grupo do Instituto de Tecnologia de Massachusetts conduziu seus próprios testes e concluiu que a arma espelho era uma possibilidade.
^[2], embora testes posteriores de seu sistema tenham demonstrado que era ineficaz em condições que mais coincidiam com o cerco descrito. O programa de TV Caçadores de Mitos Ele também assumiu o desafio de recriar a arma e concluiu que, embora fosse possível colocar fogo em um navio, ele teria que estar estacionário a uma distância especificada durante a parte mais quente de um dia muito claro e quente, e exigiria várias centenas de soldados mirando cuidadosamente. espelhos durante o ataque. Essas condições improváveis, combinadas com a disponibilidade de outros métodos mais simples, como bestas de parafuso flamejante, levaram a equipe a acreditar que o feixe de calor era muito impraticável para ser usado, e provavelmente apenas um mito.^[3]

Princípio de Arquimedes

A história de Arquimedes que descobriu a flutuabilidade enquanto estava sentado em sua banheira é descrita no Livro 9 de Por architectura por Vitruvio.
O rei Hiero deu a um ourives a quantidade exata de ouro para fazer uma coroa sagrada de ouro. Quando Hieron a recebeu, a coroa tinha o peso correto, mas o monarca suspeitou que alguma prata havia sido usada em vez de ouro. Como ele não poderia provar isso sem destruir a coroa, ele colocou o problema para Arquimedes. Um dia, ao considerar a questão, “o homem sábio” entrou em sua banheira e reconheceu que a quantidade de água que transbordava era proporcional à quantidade de seu corpo que estava submerso. Esta observação é agora conhecida como Princípio de Arquimedes e deu-lhe os meios para medir a massa da coroa de ouro. Ele estava tão animado que correu nu pelas ruas de Syracuse gritando “Eureka! Eureka!” (Encontrei-o!). O ourives desonesto foi levado à justiça.

A lei da flutuabilidade:

A força de empuxo é igual ao peso do fluido deslocado.

O peso do fluido deslocado é diretamente proporcional ao volume do fluido deslocado (especificamente se o fluido circundante tiver densidade uniforme). Assim, entre objetos de igual massa, aquele com o maior volume tem a maior flutuabilidade.

Suponha que o peso de uma rocha seja medido como 10 newtons quando ela é suspensa por uma corda no vácuo. Suponha que quando a corda abaixa a rocha na água, ela desloca a água com um peso de 3 newtons. A força exercida na corda da qual está pendurado será de 10 newtons menos os 3 newtons da força de empuxo: 10 – 3 = 7 newtons.

A densidade do objeto submerso em relação à densidade do fluido é facilmente calculada sem medir qualquer volume:

${ displaystyle { mbox {Densidade relativa}} = { frac { mbox {Peso}} {{ mbox {Peso}} – { mbox {Peso aparente submerso}}}}}$

Matemática

Em criatividade e percepção, Arquimedes superou qualquer outro matemático europeu antes do Renascimento europeu. Em uma civilização com um sistema de numeração estranho e uma linguagem em que “uma miríade” (literalmente “dez mil”) significava “infinito”, ele inventou um sistema de numeração posicional e o usou para escrever números até 10.⁶⁴. Ele desenvolveu um método heurístico baseado em estatísticas para fazer cálculos privados que hoje seriam classificados como cálculo integral, mas depois apresentou testes geométricos rigorosos para seus resultados. Até que ponto a versão de Arquimedes do cálculo integral estava correta é discutível. Ele mostrou que a razão entre a circunferência de um círculo e seu diâmetro é a mesma que a razão entre a área do círculo e o quadrado do raio. Ele não chamou essa relação de Pi (π), mas deu um procedimento para aproximá-la com precisão arbitrária e deu uma aproximação entre 3 + 10/71 (aproximadamente 3,1408) e 3 + 1/7 (aproximadamente 3,1429). Ele foi o primeiro matemático grego a introduzir curvas mecânicas (aquelas desenhadas por um ponto móvel) como objetos legítimos de estudo. Ele mostrou que a área delimitada por uma parábola e uma linha reta é 4/3 da área de um triângulo com a mesma base e altura. (Veja a ilustração abaixo. A “base” é qualquer linha secante, não necessariamente ortogonal ao eixo da parábola; “a mesma base” significa o mesmo componente “horizontal” do comprimento da base; “horizontal” significa ortogonal ao eixo. “Altura” significa o comprimento do segmento paralelo ao eixo do vértice à base. O vértice deve ser posicionado de forma que as duas distâncias horizontais mencionadas na ilustração sejam iguais.)

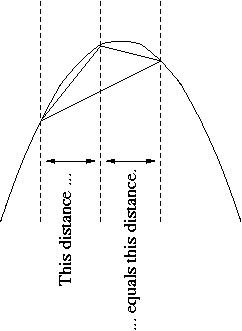
No processo, ele calculou o exemplo mais antigo conhecido de uma progressão geométrica adicionada ao infinito com a razão 1/4:

${ Displaystyle sum _ {n = 0} ^ { infty} 4 ^ {- n} = 1 + 4 ^ {- 1} +4 ^ {- 2} +4 ^ {- 3} + cdots = { 4 sobre 3} ;.}$

Se o primeiro termo nesta série é a área do triângulo na ilustração, o segundo é a soma das áreas de dois triângulos cujas bases são as duas menores linhas secantes na ilustração e assim por diante. Arquimedes também deu uma prova bastante diferente de quase a mesma proposição por um método que usa infinitesimais (ver “Uso de Infinitesimais por Arquimedes”).

Ele mostrou que a proporção da área de uma esfera para a área de um cilindro direito circunscrito é a mesma que a proporção do volume da esfera para o volume do cilindro direito circunscrito, um feito que ele havia inscrito como seu epitáfio em sua lápide.^[4]

Arquimedes é provavelmente também o primeiro físico matemático registrado, e o melhor até Galileu e Newton. Ele inventou o campo da estática, declarou a lei da alavanca, a lei do equilíbrio dos fluidos e a lei da flutuabilidade. Ele foi o primeiro a identificar o conceito de centro de gravidade e encontrou os centros de gravidade de várias figuras geométricas, incluindo triângulos, parabolóides e hemisférios, assumindo a densidade uniforme de seus interiores. Usando apenas a geometria grega antiga, ele também deu as posições de equilíbrio das seções flutuantes dos parabolóides com base em sua altura, um feito que seria desafiador para um físico moderno que usa cálculo.

Astronomia

Arquimedes também era astrônomo. Cícero escreveu que o cônsul romano Marcelo trouxe dois dispositivos da cidade saqueada de Siracusa para Roma. Um dispositivo mapeou o céu em uma esfera e o outro previu os movimentos do sol, da lua e dos planetas (um planetário). Ele credita a Thales e Eudoxus por construir esses dispositivos. Por algum tempo, a verdade dessa lenda esteve em dúvida, mas a recuperação de um antigo naufrágio em 1902 do mecanismo de Antikythera, um dispositivo datado entre 150 e 100 aC, confirmou a probabilidade de que Arquimedes possuía e construía tais dispositivos. Pappus de Alexandria escreve que Arquimedes escreveu um livro prático sobre a construção de tais esferas intitulado Sobre a fabricação de esferas.

Escritos de Arquimedes

• No equilíbrio dos aviões (2 volumes)

Este pergaminho explica a lei da alavanca e a usa para calcular as áreas e centros de gravidade de várias figuras geométricas.

Nesse pergaminho, Arquimedes define o que agora é chamado de espiral de Arquimedes, a primeira curva mecânica (curva desenhada por um ponto móvel) já considerada por um matemático grego.

• Sobre a esfera e cilindro

Neste pergaminho, Arquimedes mostra que a proporção da área de uma esfera para a de um cilindro direito circunscrito é a mesma que a do volume da esfera para o volume do cilindro (exatamente 2/3).

Neste pergaminho, Arquimedes calcula as áreas e volumes de seções de cones, esferas e parabolóides.

• Em corpos flutuantes (2 volumes)

Na primeira parte deste pergaminho, Arquimedes explica a lei do equilíbrio de fluidos e mostra que a água terá uma forma esférica em torno de um centro de gravidade. Provavelmente foi uma tentativa de explicar a observação feita por astrônomos gregos de que a Terra é redonda. Seus fluidos não gravitavam por si mesmos: assumia a existência de um ponto para o qual todas as coisas caem e derivava a forma esférica.

Na segunda parte, você calculou as posições de equilíbrio das seções parabolóides. Provavelmente foi uma idealização das formas dos cascos dos navios. Algumas de suas seções flutuam com a base sob a água e o topo acima da água, o que é uma reminiscência da forma como os icebergs flutuam.

• Quadrando a parábola

Neste rolo, Arquimedes calcula a área de um segmento de uma parábola (a figura delimitada por uma parábola e uma linha secante não necessariamente perpendicular ao eixo). A resposta final é obtida triangulando a área e somando as séries geométricas com razão de 1/4.

Este é um quebra-cabeça grego semelhante a um Tangram, e pode ser a primeira referência a este jogo. Arquimedes calcula as áreas das diferentes peças. Descobertas recentes indicam que Arquimedes estava tentando determinar de quantas maneiras as tiras de papel poderiam ser montadas em um formato quadrado. Este é possivelmente o primeiro uso da combinatória para resolver um problema.

• Problema de gado de Arquimedes

Arquimedes escreveu uma carta aos estudiosos da Biblioteca de Alexandria, que aparentemente minimizaram a importância das obras de Arquimedes. Nesta carta, ele os desafia a contar o número de gado no rebanho do Sol resolvendo uma série de equações diofantinas simultâneas, algumas delas quadráticas (na versão mais complicada). Este problema foi resolvido recentemente com a ajuda de um computador. A solução é um número muito grande, aproximadamente 7,760271 × 10²⁰⁶⁵⁴⁴ (Veja links externos para o problema do gado).

Neste pergaminho, Arquimedes conta o número de grãos de areia que podem caber dentro do universo. Este livro menciona a teoria do sistema solar de Aristarco de Samos, concluindo que é impossível, e as idéias contemporâneas sobre o tamanho da Terra e a distância entre os vários corpos celestes.

Este trabalho, que era desconhecido na Idade Média, mas cuja importância foi percebida após sua descoberta, foi pioneiro no uso de infinitesimais, mostrando como dividir uma figura em um número infinito de partes infinitamente pequenas poderia ser usado para determinar sua área ou volume. Arquimedes provavelmente considerou esses métodos não matematicamente precisos e os usou para encontrar pelo menos algumas das áreas ou volumes que estava procurando, e então usou o método mais tradicional de esgotamento para testá-los.

Notas

Referências

• Arquimedes; Sir Thomas Heath, (tradutor). As obras de Arquimedes. reimpresso ed. Dover Publications 2002. ISBN 0486420841
• Arquimedes; Reviel Netz. As obras de Arquimedes: tradução e comentário. Cambridge University Press, 2004. ISBN 0521661609
• Dijksterhuis, E. J. Arquimedes. Princeton, Princeton University Press, 1987. ISBN 0691084211.
• Kliner, Fred S.; Mamiya, Kliner Christin J .. “A Arte do Jardineiro Através dos Séculos”, décima segunda ed. Vol II. Los Angeles: Thompson Wadsworth, 2005.
• Laubenbacher, Reinhard e David Pengelley. Expedições matemáticas: Crônicas dos exploradores. 1999. ISBN 0387984348
• Plutarco. Vidas de Plutarco, traduzido por John Dryden. Nova York: Modern Library, ASIN: B000RS0LX6
• Stadter, Philip A. Los métodos históricos de Plutarco: un análisis de los Mulierum virtutes. Harvard University Press, 1965. ASIN: B0007DKTAG

Introducción para adultos jóvenes

• Benkick, Jeanne. Arquímedes y la puerta a la ciencia. Libros de Belén, 1995. ISBN 1883937124
• Zannos, Susan. La vida y los tiempos de Arquímedes. (Biografía de civilizaciones antiguas) Mitchell Lane Publishers, 2004. ISBN 1584152427

links externos

Todos los enlaces se recuperaron el 12 de abril de 2016.